W matematyce jednym z podstawowych pojęć jest wyrażanie skomplikowanych wyrażeń w prostszych formach. Ten proces nosi nazwę "rozkład wyrażenia wymiernego na ułamki proste". Poprzez rozkładanie skomplikowanych wyrażeń na proste ułamki, matematycy i uczniowie mogą lepiej zrozumieć i manipulować podstawowymi strukturami matematycznymi. W tym artykule omówimy pojęcie rozkładu wyrażenia wymiernego na ułamki proste, zapewniając krok po kroku wyjaśnienia i przykłady, które zwiększą Twoje zrozumienie.
Czym jest Rozkład Wyrażenia Wymiernego na Ułamki Proste?
Rozkład wyrażenia wymiernego na ułamki proste to proces w matematyce, który polega na rozkładaniu wyrażenia wymiernego na sumę prostych ułamków. Wyrażenie wymierne to ułamek, w którym w liczniku i mianowniku występują wielomiany. Poprzez rozkładanie wyrażenia na prostsze ułamki, możemy analizować jego poszczególne składniki i łatwiej wykonywać operacje na tych wyrażeniach.
Kroki Rozkładu Wyrażenia Wymiernego na Ułamki Proste
Aby rozłożyć wyrażenie wymierne na proste ułamki, wykonujemy szereg kroków. Przeanalizujmy każdy krok dokładniej:
Krok 1: Rozkładanie Mianownika na Czynniki
Pierwszym krokiem w rozkładzie wyrażenia wymiernego na ułamki proste jest rozłożenie mianownika na czynniki. Poprzez rozłożenie mianownika, możemy zidentyfikować poszczególne czynniki, które wpływają na całe wyrażenie.
Krok 2: Określanie Prostych Ułamków
Po rozłożeniu mianownika określamy proste ułamki, które stanowią wyrażenie wymierne. Każdy prosty ułamek odpowiada jednemu z czynników otrzymanych we wcześniejszym kroku.
Krok 3: Zapisywanie Rozkładu
W tym kroku zapisujemy rozkład wyrażenia wymiernego jako sumę prostych ułamków. Rozkład pozwala nam przedstawić skomplikowane wyrażenie za pomocą prostszych ułamków.
Krok 4: Określanie Nieznanych Współczynników
Ostatnim krokiem jest określenie nieznanych współczynników w prostych ułamkach. Aby to zrobić, równujemy oryginalne wyrażenie wymierne z rozkładem i rozwiązujemy równania, aby znaleźć wartości współczynników przy ułamkach. Techniki algebraiczne potrzebne do rozwiązania równań zależą od złożoności wyrażenia.
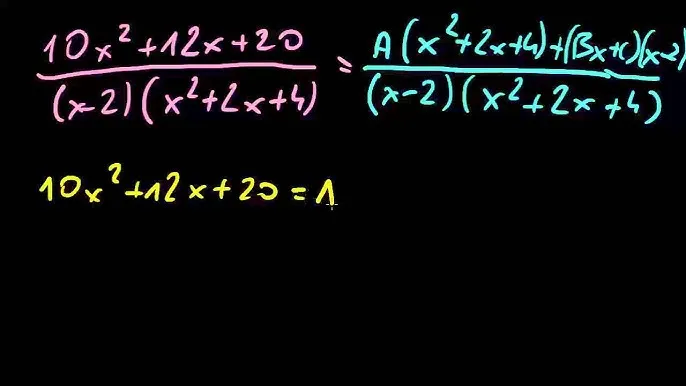
Przykład: Rozkładanie Wyrażenia Wymiernego
Przeanalizujmy proces rozkładania wyrażenia wymiernego na proste ułamki na przykładzie. Rozważmy wyrażenie wymierne:
R(x) = (3x + 2) / (x^2 + x - 2)
Krok 1: Rozkładanie Mianownika na Czynniki
Zaczynamy od rozłożenia mianownika (x^2 + x - 2). Możemy go rozłożyć na czynniki jako (x + 2)(x - 1).
Krok 2: Określanie Prostych Ułamków
Następnie określamy proste ułamki odpowiadające czynnikom (x + 2) i (x - 1). Oznaczmy je jako A i B:
R(x) = A / (x + 2) + B / (x - 1)
Krok 3: Zapisywanie Rozkładu
Zapisujemy rozkład wyrażenia wymiernego za pomocą prostych ułamków:
R(x) = A / (x + 2) + B / (x - 1)
Krok 4: Określanie Nieznanych Współczynników
Aby określić nieznane współczynniki A i B, równujemy oryginalne wyrażenie wymierne z rozkładem:
(3x + 2) / (x^2 + x - 2) = A / (x + 2) + B / (x - 1)
Poprzez przemnożenie obu stron przez wspólny mianownik (x + 2)(x - 1), możemy wyeliminować ułamki i rozwiązać równania, aby znaleźć współczynniki A i B. Konkretne techniki algebraiczne wymagane do rozwiązania równań zależą od złożoności wyrażenia.
