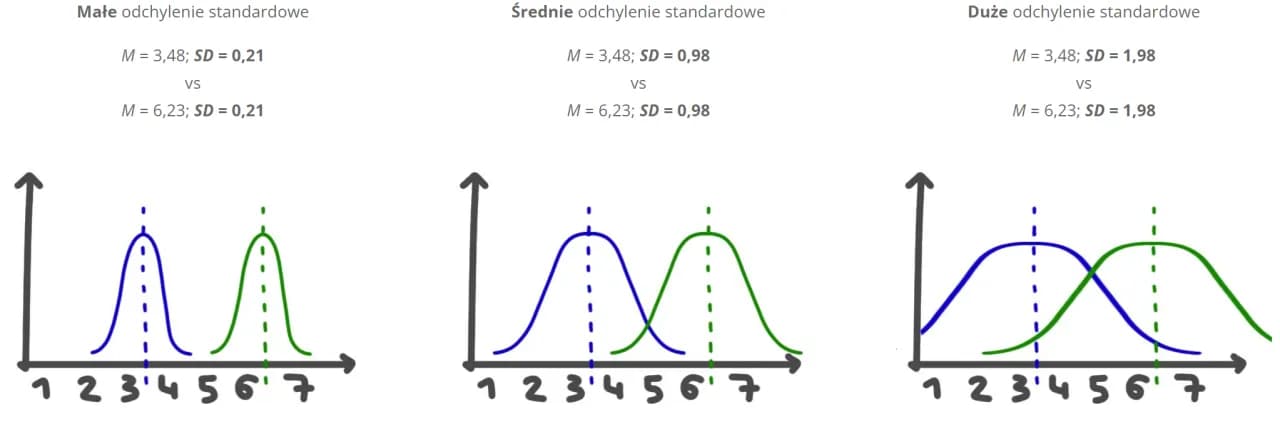
Odchylenie standardowe to fundamentalna miara statystyczna, która pokazuje rozproszenie danych wokół średniej. Pomaga zrozumieć, jak bardzo wartości w zbiorze różnią się od siebie. Im mniejsza wartość odchylenia, tym dane są bardziej skupione wokół średniej. Większe wartości wskazują na znaczące różnice między pomiarami.
Oznaczane jako σ dla populacji lub s dla próby, odchylenie standardowe znajduje zastosowanie w wielu dziedzinach. Jest kluczowe w analizie danych, badaniach naukowych i statystyce. Pozwala ocenić wiarygodność wyników i wykryć nietypowe wartości.
Najważniejsze informacje:- Małe odchylenie = dane skupione blisko średniej
- Duże odchylenie = znaczne rozproszenie danych
- Służy do wykrywania wartości odstających (outlierów)
- Umożliwia porównywanie zmienności różnych zbiorów danych
- Jest niezbędne w analizie statystycznej i interpretacji wyników badań
Czym jest odchylenie standardowe w praktyce?
Odchylenie standardowe to podstawowa miara rozproszenia danych wokół średniej. Znaczenie odchylenia standardowego w statystyce jest kluczowe dla zrozumienia zmienności wyników. Pozwala określić, jak bardzo wartości odbiegają od średniej w zbiorze danych.
Jak obliczać odchylenie standardowe? Obliczamy je jako pierwiastek kwadratowy z wariancji, która jest średnią kwadratów różnic między wartościami a średnią arytmetyczną. Oznaczamy je symbolem σ dla populacji lub s dla próby. W praktyce, im większa wartość odchylenia, tym większe rozproszenie danych.
- Miara rozproszenia wartości wokół średniej
- Pierwiastek kwadratowy z wariancji
- Wskaźnik zmienności danych
- Narzędzie do wykrywania wartości odstających
Jak odczytywać wartości odchylenia standardowego?
Analiza odchylenia standardowego w praktyce wymaga odniesienia do średniej. Przy odchyleniu 5 lat i średniej wieku 40 lat, większość obserwacji mieści się między 35 a 45 lat. To pokazuje, jak szczelnie dane grupują się wokół średniej.
W przypadku wyników testów ze średnią 75 punktów i odchyleniem 10 punktów, około 68% uczniów uzyskało wynik między 65 a 85 punktów. Jeszcze szerszy zakres - dwa odchylenia standardowe (55-95 punktów) - obejmuje już około 95% wszystkich wyników.
Interpretując dane finansowe, przy średnim zwrocie z inwestycji 8% i odchyleniu 2%, typowe wyniki mieszczą się w przedziale 6-10%. To pozwala ocenić ryzyko inwestycyjne.
Małe vs duże odchylenie standardowe - co to oznacza?
Odchylenie standardowe przykłady najlepiej pokazują różnice w rozproszeniu danych. Małe odchylenie (np. 1-2% przy średniej 10%) wskazuje na stabilne, przewidywalne wyniki. Duże odchylenie (np. 15-20%) sugeruje znaczną zmienność i niepewność.
W przypadku wzrostu populacji, odchylenie 5 cm przy średniej 170 cm oznacza niewielką zmienność. Natomiast odchylenie 20 cm wskazywałoby na bardzo zróżnicowaną grupę.
| Zbiór danych | Średnia | Odchylenie | Interpretacja |
|---|---|---|---|
| Wiek pracowników | 35 lat | 3 lata | Jednolita grupa wiekowa |
| Wynagrodzenia | 5000 zł | 1500 zł | Umiarkowane zróżnicowanie |
| Zwroty z inwestycji | 12% | 25% | Wysoka zmienność |
Kiedy odchylenie standardowe jest małe?
Małe odchylenie standardowe występuje, gdy dane są skupione blisko średniej. W produkcji przemysłowej, odchylenie 0.1mm przy średniej 10mm świadczy o wysokiej precyzji procesu. Taka sytuacja jest pożądana w kontroli jakości.
Przykładem są też wyniki egzaminów w klasie o wyrównanym poziomie. Przy średniej 80 punktów i odchyleniu 5 punktów, większość uczniów osiąga wyniki między 75 a 85 punktów. To wskazuje na jednorodną grupę.
Kiedy odchylenie standardowe jest duże?
Duże odchylenie standardowe pojawia się przy znacznym rozproszeniu danych. W badaniach dochodów gospodarstw domowych, odchylenie 5000 zł przy średniej 8000 zł pokazuje duże różnice ekonomiczne. Świadczy to o nierównomiernym rozkładzie zarobków.
Inny przykład to pomiary temperatury rocznej, gdzie odchylenie 15°C przy średniej 20°C wskazuje na klimat z wyraźnymi różnicami sezonowymi. Takie wartości są typowe dla klimatu umiarkowanego.
Jak wykorzystać odchylenie standardowe w analizie danych?
Zastosowanie odchylenia standardowego jest szerokie i praktyczne. W finansach służy do oceny ryzyka inwestycyjnego - większe odchylenie oznacza wyższe ryzyko. W medycynie pomaga określić granice norm dla wyników badań.
W kontroli jakości produkcji pozwala ustalić dopuszczalne granice tolerancji. Przykładowo, przy produkcji części mechanicznych odchylenie 0.05mm może być maksymalną akceptowalną wartością.
Badania marketingowe wykorzystują tę miarę do analizy zachowań konsumentów. Duże odchylenie w wydatkach na dane produkty może sugerować zróżnicowane preferencje klientów.
- Analiza ryzyka finansowego
- Kontrola jakości w produkcji
- Badania medyczne i normy laboratoryjne
- Analiza wyników testów i egzaminów
- Badania rynku i zachowań konsumenckich
Odchylenie standardowe w różnych dziedzinach
Jak interpretować odchylenie standardowe zależy od kontekstu branżowego. W meteorologii służy do analizy zmienności pogody, gdzie odchylenie 5°C jest normalne dla temperatur miesięcznych. W sporcie pomaga ocenić stabilność wyników zawodników.
W przemyśle farmaceutycznym określa dokładność dozowania leków. Odchylenie nie może przekraczać 1% zawartości substancji czynnej. To kluczowe dla bezpieczeństwa pacjentów.
Sektor ubezpieczeń wykorzystuje tę miarę do szacowania ryzyka i kalkulacji składek. Większe odchylenie w statystykach wypadków oznacza wyższe składki ubezpieczeniowe.
W rolnictwie analizuje się zmienność plonów. Odchylenie standardowe 15% przy średniej wydajności może wskazywać na wpływ czynników klimatycznych.
Zastosowanie w finansach
Jak interpretować odchylenie standardowe w kontekście finansowym? Przy analizie portfela inwestycyjnego odchylenie 12% przy średnim zwrocie 10% wskazuje na podwyższone ryzyko. Większe odchylenie oznacza większą zmienność zwrotów.
W bankowości, analizując zdolność kredytową, odchylenie w miesięcznych dochodach klienta na poziomie 20% może sygnalizować niestabilność finansową. Przy średnim dochodzie 6000 zł, wahania między 4800 a 7200 zł wpływają na ocenę ryzyka kredytowego.
Zastosowanie w badaniach naukowych
Analiza odchylenia standardowego w praktyce naukowej jest fundamentalna. W badaniach klinicznych, odchylenie 5 jednostek przy średnim efekcie leku 50 jednostek pokazuje stabilność działania preparatu. To kluczowe przy ocenie skuteczności terapii.
W badaniach psychologicznych, przy pomiarze czasu reakcji, odchylenie 0.2 sekundy przy średniej 0.8 sekundy wskazuje na spójność wyników. Większe odchylenia mogą sugerować problemy z koncentracją badanych osób.
Typowe wartości odchylenia standardowego
Odchylenie standardowe przykłady różnią się znacząco między dziedzinami. W pomiarach wzrostu dorosłych typowe odchylenie to około 7 cm. Dla wagi często wynosi około 15 kg.
W testach IQ standardowe odchylenie ustalone jest na 15 punktów przy średniej 100. To pozwala łatwo interpretować wyniki w kontekście populacji.
Dla temperatur dziennych w klimacie umiarkowanym typowe odchylenie to około 5-8°C w skali roku. Miesięczne odchylenia są zwykle mniejsze.
| Rodzaj danych | Typowe odchylenie | Kontekst |
|---|---|---|
| IQ | 15 punktów | Standaryzowany test |
| Wzrost dorosłych | 7 cm | Populacja ogólna |
| Wyniki egzaminów | 10-15% | Skala 100-punktowa |
Związek z innymi miarami statystycznymi
Znaczenie odchylenia standardowego w statystyce jest ściśle powiązane z innymi miarami. Kwadrat odchylenia daje wariancję, która jest podstawową miarą zmienności.
Współczynnik zmienności to stosunek odchylenia do średniej, wyrażony w procentach. Przy średniej sprzedaży 1000 sztuk i odchyleniu 200, współczynnik zmienności wynosi 20%, co wskazuje na umiarkowaną zmienność.
W rozkładzie normalnym, przedziały ufności bazują na odchyleniu standardowym. Przy średniej 100 i odchyleniu 15, przedział 85-115 obejmuje około 68% obserwacji. To podstawa wielu analiz statystycznych.
Co musisz wiedzieć o odchyleniu standardowym?
Odchylenie standardowe to więcej niż tylko matematyczna formuła - to praktyczne narzędzie do zrozumienia zmienności danych. Niezależnie czy analizujesz wyniki finansowe, badania naukowe czy produkcję przemysłową, znajomość tej miary pomoże Ci podejmować lepsze decyzje. Małe odchylenie oznacza stabilność i przewidywalność, podczas gdy duże wskazuje na znaczące różnice w danych.
W praktyce, interpretacja odchylenia standardowego zawsze zależy od kontekstu. Wartość 5% może być alarmująca w kontroli jakości leków, ale całkowicie akceptowalna w analizie zwrotów z inwestycji. Kluczowe jest odniesienie odchylenia do średniej i specyfiki badanego zjawiska. Wykorzystanie reguły 68-95-99 znacząco ułatwia interpretację wyników w każdej dziedzinie.
Pamiętaj, że analiza odchylenia standardowego w praktyce to nie tylko liczby - to sposób na zrozumienie ryzyka, jakości i zmienności w twoich danych. Im lepiej rozumiesz tę miarę, tym trafniejsze decyzje możesz podejmować w swojej dziedzinie.