Korelacja i zależność to dwa ważne pojęcia w statystyce i analizie danych. Choć często używane zamiennie, mają różne znaczenia i zastosowania. Korelacja opisuje statystyczny związek między zmiennymi, pokazując, jak zmiany w jednej wpływają na drugą. Nie oznacza to jednak przyczynowości. Z kolei zależność to szersze pojęcie, obejmujące różne rodzaje relacji między zmiennymi, w tym przyczynowe i nieliniowe. Zrozumienie różnicy między tymi terminami jest kluczowe dla prawidłowej interpretacji danych i wyników analiz statystycznych.
Najważniejsze informacje:- Korelacja mierzy współwystępowanie zmiennych, ale nie wskazuje na przyczynowość
- Zależność obejmuje wszelkie relacje między zmiennymi, w tym przyczynowe i nieliniowe
- Korelacja może być dodatnia, ujemna lub zerowa
- Zależności często wymagają bardziej złożonej analizy niż korelacje
- Prawidłowe rozróżnienie tych pojęć jest istotne w analizie danych
Czym jest korelacja w analizie danych?
Korelacja to statystyczna miara związku między dwiema zmiennymi. Pokazuje, jak zmiany w jednej zmiennej są powiązane ze zmianami w drugiej.
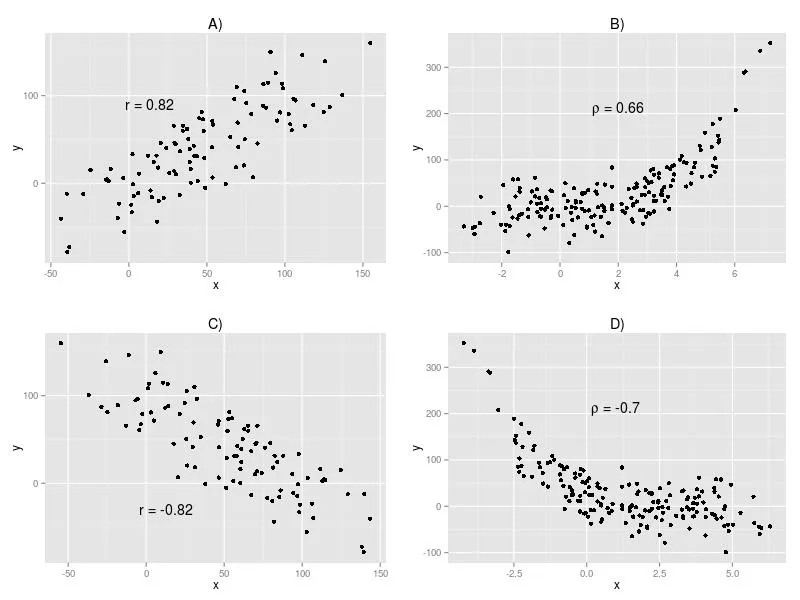
Współczynnik korelacji to liczba określająca siłę i kierunek tego związku. Przyjmuje wartości od -1 do 1, gdzie -1 oznacza idealną korelację ujemną, 0 brak korelacji, a 1 idealną korelację dodatnią. Najczęściej używanym jest współczynnik korelacji Pearsona.Interpretacja współczynnika korelacji jest kluczowa w analizie korelacji. Wartości bliskie -1 lub 1 wskazują na silny związek, podczas gdy wartości bliskie 0 sugerują słaby związek lub jego brak. Jednak pamiętajmy, że korelacja nie oznacza przyczynowości. Dwie zmienne mogą być skorelowane bez bezpośredniego wpływu na siebie.
Rodzaje korelacji
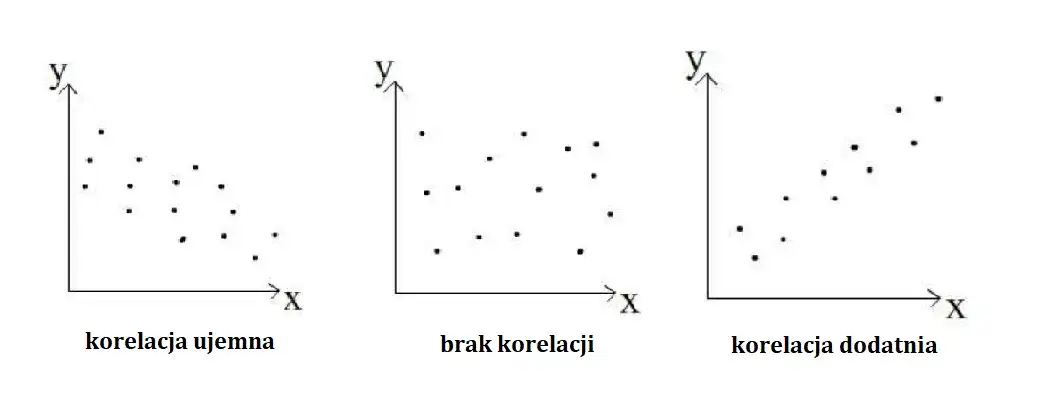
- Korelacja dodatnia
- Korelacja ujemna
- Brak korelacji
Korelacja dodatnia występuje, gdy wzrost jednej zmiennej wiąże się ze wzrostem drugiej. Przykładem może być związek między czasem nauki a wynikami egzaminów.
Korelacja ujemna oznacza, że wzrost jednej zmiennej wiąże się ze spadkiem drugiej. Ilustruje to relacja między cenami a popytem na towary luksusowe.
Brak korelacji wskazuje na brak liniowego związku między zmiennymi. Na przykład, kolor samochodu nie ma związku z jego zużyciem paliwa.
Zależność - szersze spojrzenie na relacje między zmiennymi
Zależność statystyczna to ogólniejsze pojęcie niż korelacja. Obejmuje wszelkie relacje między zmiennymi, niekoniecznie liniowe czy proporcjonalne.
W przeciwieństwie do korelacji, zależność może obejmować związki przyczynowe i bardziej złożone interakcje. Analiza zależności często wymaga zaawansowanych technik statystycznych i modelowania, wykraczających poza prostą korelację.
Typy zależności
Zależność przyczynowa występuje, gdy zmiany w jednej zmiennej bezpośrednio wpływają na drugą. Wymaga ona dokładnej analizy i kontroli czynników zewnętrznych. Zrozumienie zależności przyczynowych jest kluczowe w badaniach naukowych i podejmowaniu decyzji biznesowych.
Zależność nieliniowa to relacja, w której zmiany w jednej zmiennej nie są proporcjonalne do zmian w drugiej. Może mieć różne formy, takie jak zależności kwadratowe czy wykładnicze. Analiza takich zależności wymaga bardziej zaawansowanych narzędzi statystycznych.
Przykładem zależności przyczynowej jest wpływ szczepień na zachorowalność. Zależność nieliniową ilustruje relacja między wiekiem a zdolnością uczenia się nowych języków.
Czytaj więcej: Najlepsze książki o analizie fundamentalnej: Kompletny przegląd
Kluczowe różnice między korelacją a zależnością
| Kryterium | Korelacja | Zależność |
|---|---|---|
| Zakres | Tylko związki liniowe | Wszelkie rodzaje związków |
| Przyczynowość | Nie implikuje | Może obejmować |
| Mierzalność | Łatwo mierzalna (współczynnik) | Trudniejsza do zmierzenia |
| Interpretacja | Prosta (-1 do 1) | Złożona, kontekstowa |
| Zastosowanie | Wstępna analiza danych | Głębsza analiza i modelowanie |
Korelacja a zależność różnią się przede wszystkim zakresem analizy. Korelacja skupia się na liniowych związkach, podczas gdy zależność obejmuje szerszy spektrum relacji. To kluczowa różnica w interpretacji danych.
Kolejna istotna różnica dotyczy przyczynowości. Korelacja nie implikuje związku przyczynowego, natomiast analiza zależności może obejmować badanie przyczyn i skutków. To ważne w kontekście podejmowania decyzji opartych na danych.
Wreszcie, metody analizy i interpretacji różnią się znacząco. Korelacja oferuje prostą miarę liczbową, podczas gdy badanie zależności często wymaga bardziej zaawansowanych technik statystycznych i głębszego zrozumienia kontekstu danych.
Jak interpretować korelację w kontekście zależności?
Interpretacja korelacji wymaga ostrożności, szczególnie w kontekście zależności. Silna korelacja nie oznacza automatycznie istnienia związku przyczynowego. Mogą istnieć ukryte zmienne wpływające na obie badane cechy. Dlatego kluczowe jest rozróżnienie między korelacją a przyczynowością.
Klasycznym przykładem błędnej interpretacji jest związek między sprzedażą lodów a liczbą utonięć. Choć dane mogą wykazywać silną korelację dodatnią, nie oznacza to, że jedzenie lodów powoduje utonięcia. W rzeczywistości, oba zjawiska są związane z ukrytą zmienną - wysoką temperaturą w lecie.
Zastosowania korelacji i zależności w analizie danych
Obszary zastosowań korelacji:
- Analiza rynku finansowego
- Badania marketingowe
- Prognozowanie pogody
- Analiza wyników sportowych
- Badania medyczne
Obszary zastosowań analizy zależności:
- Modelowanie ekonometryczne
- Badania nad efektywnością leków
- Analiza zachowań konsumenckich
- Badania społeczne
- Optymalizacja procesów produkcyjnych
Korelacja jest często stosowana w szybkich analizach rynkowych i finansowych. Pozwala na identyfikację potencjalnych związków między zmiennymi ekonomicznymi.
Analiza zależności znajduje zastosowanie w bardziej złożonych badaniach naukowych. Umożliwia głębsze zrozumienie mechanizmów stojących za obserwowanymi zjawiskami.
Różnica w zastosowaniu polega głównie na głębokości analizy i wymaganych zasobach. Korelacja oferuje szybki wgląd, podczas gdy badanie zależności wymaga bardziej zaawansowanych metod i dłuższego czasu.
Ograniczenia korelacji w badaniu zależności
- Niemożność ustalenia kierunku przyczynowości.
- Wrażliwość na wartości odstające.
- Ograniczenie do związków liniowych.
- Możliwość istnienia korelacji pozornych.
Brak możliwości określenia kierunku przyczynowości stanowi poważne ograniczenie korelacji. Silna korelacja między dwiema zmiennymi nie mówi nam, która z nich jest przyczyną, a która skutkiem. To utrudnia wyciąganie wniosków o rzeczywistych zależnościach.
Wrażliwość na wartości odstające może prowadzić do błędnych interpretacji. Pojedyncze, ekstremalne obserwacje mogą znacząco wpłynąć na wartość współczynnika korelacji, zniekształcając obraz rzeczywistego związku między zmiennymi.
Ograniczenie do związków liniowych sprawia, że korelacja może nie wykryć istotnych, ale nieliniowych zależności. Wiele zjawisk w rzeczywistości charakteryzuje się złożonymi, nieliniowymi relacjami, których prosta korelacja nie jest w stanie uchwycić.
Możliwość wystąpienia korelacji pozornych to kolejne ważne ograniczenie. Dwie zmienne mogą wykazywać silną korelację, mimo braku rzeczywistego związku przyczynowego, ze względu na wpływ nieuwzględnionych czynników zewnętrznych.
Zaawansowane metody badania zależności
Analiza zależności wykracza daleko poza prostą korelację. Zaawansowane metody pozwalają na głębsze zrozumienie złożonych relacji między zmiennymi.
Analiza regresji wielorakiej umożliwia badanie wpływu wielu zmiennych niezależnych na zmienną zależną. Pozwala to na kontrolowanie wpływu różnych czynników i identyfikację tych najistotniejszych. Metoda ta jest szeroko stosowana w ekonometrii, naukach społecznych i badaniach medycznych, umożliwiając tworzenie modeli predykcyjnych i wyjaśniających.
Analiza szeregów czasowych to potężne narzędzie do badania zależności w danych zmieniających się w czasie. Umożliwia identyfikację trendów, sezonowości i cykliczności. Metody takie jak ARIMA czy analiza spektralna pozwalają na modelowanie złożonych wzorców czasowych i prognozowanie przyszłych wartości, co jest kluczowe w analizie finansowej czy prognozowaniu pogody.Modele równań strukturalnych (SEM) umożliwiają badanie złożonych zależności przyczynowych między wieloma zmiennymi. Łączą one elementy analizy czynnikowej i regresji wielorakiej. SEM pozwala na testowanie hipotez o skomplikowanych relacjach między zmiennymi obserwowalnymi i ukrytymi, co jest szczególnie cenne w psychologii, socjologii i badaniach marketingowych.
Dlaczego rozróżnianie korelacji i zależności jest kluczowe?
Prawidłowe rozróżnianie korelacji a zależności jest fundamentalne dla rzetelnej interpretacji wyników badań. Pozwala uniknąć błędnych wniosków i nadinterpretacji danych. Świadomość różnic między tymi pojęciami chroni przed wyciąganiem nieuprawnionych wniosków przyczynowo-skutkowych.
Zrozumienie natury związków między zmiennymi ma ogromny wpływ na podejmowanie decyzji. W biznesie, medycynie czy polityce, błędne założenie o przyczynowości na podstawie samej korelacji może prowadzić do kosztownych lub nawet niebezpiecznych decyzji. Dokładna analiza zależności pozwala na bardziej świadome i efektywne działania.
Rozróżnianie korelacji a zależności napędza rozwój nauki i innowacji w biznesie. Prowadzi do formułowania bardziej precyzyjnych hipotez badawczych i poszukiwania głębszych związków przyczynowych. W rezultacie przyczynia się do lepszego zrozumienia złożonych zjawisk i tworzenia skuteczniejszych rozwiązań w różnych dziedzinach.
Praktyczne wskazówki analizy korelacji i zależności
- Zawsze rozpoczynaj od wizualizacji danych.
- Rozważ wpływ zmiennych ukrytych.
- Stosuj różne miary korelacji odpowiednie do typu danych.
- Przeprowadzaj testy statystyczne dla potwierdzenia istotności korelacji.
- Wykorzystuj wiedzę dziedzinową do interpretacji wyników.
Wizualizacja danych pozwala na szybkie wykrycie potencjalnych zależności i anomalii. Wykresy rozrzutu czy mapy cieplne mogą ujawnić wzorce niewidoczne w samych liczbach.
Rozważanie wpływu zmiennych ukrytych jest kluczowe dla uniknięcia błędnych wniosków. Zawsze zastanów się, czy obserwowana korelacja nie wynika z wpływu nieuwzględnionych czynników.
Dobór odpowiedniej miary korelacji zależy od charakteru danych. Dla danych porządkowych stosuj korelację Spearmana, a dla zmiennych nominalnych - współczynnik V Cramera.
Testy statystyczne, takie jak test t dla korelacji, pomagają ocenić, czy obserwowana korelacja jest istotna statystycznie. Pamiętaj, że istotność statystyczna nie zawsze oznacza istotność praktyczną.
Wiedza dziedzinowa jest niezbędna do prawidłowej interpretacji wyników
Wiedza dziedzinowa jest niezbędna do prawidłowej interpretacji wyników analizy. Pozwala ona na ocenę, czy odkryte zależności mają sens w kontekście badanego zjawiska. Eksperci w danej dziedzinie mogą pomóc w identyfikacji potencjalnych zmiennych zakłócających i mechanizmów przyczynowych.
Korzyści z prawidłowego rozróżniania korelacji i zależności
Zrozumienie różnicy między korelacją a zależnością przynosi wiele korzyści w analizie danych. Pozwala na uniknięcie pułapek interpretacyjnych i prowadzi do głębszego wglądu w badane zjawiska.
W biznesie, prawidłowa interpretacja danych przekłada się na lepsze decyzje strategiczne. Firmy mogą uniknąć kosztownych błędów wynikających z mylenia korelacji z przyczynowością. Na przykład, zamiast inwestować w działania oparte na pozornych związkach, mogą skupić się na rzeczywistych czynnikach wpływających na wyniki.
W nauce, rozróżnianie korelacji a zależności prowadzi do formułowania bardziej precyzyjnych hipotez badawczych. Naukowcy mogą lepiej planować eksperymenty, kontrolując odpowiednie zmienne i identyfikując prawdziwe mechanizmy przyczynowe. To z kolei przyspiesza postęp naukowy i prowadzi do przełomowych odkryć.
Wyzwania w analizie korelacji i zależności
Analiza korelacji i zależności stawia przed badaczami szereg wyzwań. Jednym z nich jest problem dużej liczby zmiennych w zbiorach danych. W erze big data, identyfikacja istotnych korelacji i zależności staje się coraz trudniejsza.
Kolejnym wyzwaniem jest interpretacja wyników w kontekście złożonych systemów. Wiele zjawisk w rzeczywistości charakteryzuje się skomplikowanymi, nieliniowymi zależnościami, które trudno uchwycić za pomocą prostych miar korelacji. Wymaga to stosowania zaawansowanych technik analizy i modelowania.
Problem przyczynowości pozostaje jednym z największych wyzwań. Nawet zaawansowane metody statystyczne nie zawsze pozwalają na jednoznaczne ustalenie kierunku przyczynowości. Badacze muszą często polegać na dodatkowych źródłach informacji i eksperymentach, aby potwierdzić swoje hipotezy o zależnościach przyczynowych.
Przyszłość analizy korelacji i zależności
Rozwój sztucznej inteligencji i uczenia maszynowego otwiera nowe możliwości w analizie korelacji i zależności. Algorytmy AI mogą wykrywać subtelne wzorce i zależności w ogromnych zbiorach danych, niedostrzegalne dla tradycyjnych metod statystycznych.
Coraz większą rolę odgrywają metody przyczynowej analizy danych. Techniki takie jak modelowanie przyczynowe czy analiza kontrfaktyczna pozwalają na głębsze zrozumienie mechanizmów stojących za obserwowanymi korelacjami. To kluczowe dla podejmowania trafnych decyzji w złożonych systemach.
Interdyscyplinarne podejście do analizy danych staje się normą. Łączenie wiedzy z różnych dziedzin - statystyki, informatyki, psychologii czy ekonomii - pozwala na bardziej kompleksowe badanie zależności. Takie podejście jest szczególnie cenne w rozwiązywaniu złożonych problemów społecznych i biznesowych.
Podsumowanie
Korelacja a zależność to kluczowe pojęcia w analizie danych, których prawidłowe rozumienie jest niezbędne dla rzetelnej interpretacji wyników. Korelacja mierzy siłę liniowego związku między zmiennymi, podczas gdy zależność obejmuje szerszy zakres relacji, w tym związki przyczynowe i nieliniowe.
Świadomość różnic między tymi pojęciami chroni przed błędnymi wnioskami i pozwala na głębsze zrozumienie badanych zjawisk. W praktyce, analiza danych powinna wykraczać poza prostą korelację, wykorzystując zaawansowane metody statystyczne i wiedzę dziedzinową.
Przyszłość analizy korelacji i zależności wiąże się z rozwojem AI, metodami przyczynowej analizy danych i interdyscyplinarnym podejściem. Te trendy obiecują jeszcze dokładniejsze i bardziej użyteczne wnioski z analizy danych, co będzie miało ogromny wpływ na naukę, biznes i społeczeństwo.
Korelacja a zależność: klucz do głębszego zrozumienia danych
Rozróżnienie między korelacją a zależnością jest fundamentalne w analizie danych. Korelacja mierzy siłę liniowego związku, podczas gdy zależność obejmuje szerszy zakres relacji, włączając związki przyczynowe i nieliniowe. To rozróżnienie ma kluczowe znaczenie dla unikania błędnych interpretacji i podejmowania trafnych decyzji w nauce i biznesie.
Prawidłowa analiza wymaga nie tylko znajomości statystycznych narzędzi, ale także wiedzy dziedzinowej i krytycznego myślenia. Zaawansowane metody, takie jak analiza regresji wielorakiej czy modele równań strukturalnych, pozwalają na głębsze badanie złożonych zależności. Jednocześnie, rozwój AI i uczenia maszynowego otwiera nowe możliwości w odkrywaniu subtelnych wzorców w danych.
Świadomość ograniczeń korelacji i umiejętność stosowania odpowiednich metod analizy zależności są niezbędne dla każdego, kto pracuje z danymi. To nie tylko kwestia poprawności metodologicznej, ale także etycznej odpowiedzialności za wnioski wyciągane z analizy. W erze big data, zdolność do rozróżniania korelacji od zależności staje się kluczową kompetencją, napędzającą innowacje i pomagającą w rozwiązywaniu złożonych problemów społecznych i biznesowych.